Pythonでダイクストラ法を実装してみた

ダイクストラ法(Dijkstra’s algorithm)とは

ダイクストラ法とはグラフ理論において、
辺の重みが非負数の場合で始点が単一の最短経路問題を解くための
最良優先探索によるアルゴリズムである。
単一始点最短経路問題を解くアルゴリズムには，他にBellman–Ford法が存在するが，Bellman–Ford法は主に辺の重みに負数が含まれる場合に使われる。
辺の重みが非負数である場合には最優先キューを併用したDijkstra法の方が速い(たしか)。
計算量のオーダーはwikipediaに載ってたと思うので、そちらを参考にしてください。 ダイクストラ法のアルゴリズムについては、 また後日、記事をあげようと思います。 今回は、Pythonでダイクストラ法を実装してみました。 NetworkXのAPIにダイクストラ法が既にあるのになぜ、今更、実装したのかと言いますと、 NetworkXのダイクストラ法では、重み付き辺グラフを解くことができなかったからです。
(もしかしたら出来るかもしれません。できたらすみません🙇‍♂️) 前回、試した時には、経由するノードの数が最小になるルートしか出てこなかったです。

Pythonでのコード

今回の実装は、プログラマにとっての神サイトQiita Python ダイクストラ法 ( Dijkstra’s algorithm ) で最短経路を求める を参考に作成させていただきました。 変更点としましては、

• 開始と終点ノードを引数で指定できるようにしました。
• 調べたいグラフ(二次元リスト)を引数で指定できるようにしました。
• 孤立しているノードがあっても対応できるようにしました。
• 出力結果を見やすくしました。

以下がソースコードになります。
matrix_listがグラフ(二次元リスト)
startが開始ノード
terminalが終点ノード

def dijkstra(matrix_list,start,terminal):

    import math

    route_list = matrix_list # 初期のノード間の距離のリスト

    isolate_num = 0
    isolated_list = []
    node_num = len(route_list) #ノードの数
    unsearched_nodes = list(range(node_num)) # 未探索ノード
    distance = [math.inf] * node_num # ノードごとの距離のリスト
    previous_nodes = [-1] * node_num # 最短経路でそのノードのひとつ前に到達するノードのリスト
    distance[start] = 0 # 初期のノードの距離は0とする

    for isolate in unsearched_nodes:#孤立したノードを探索済にする
        if route_list[isolate].count(0) == node_num:
            unsearched_nodes.remove(isolate)
            distance[isolate] = -isolate

    while(len(unsearched_nodes) != 0): #未探索ノードがなくなるまで繰り返す
        possible_min_distance = math.inf # 最小のdistanceを見つけるための一時的なdistance。初期値は inf に設定。
         # まず未探索ノードのうちdistanceが最小のものを選択する
        min = math.inf
        for target in unsearched_nodes:
            if distance[target] < min:
                min = distance[target]
                target_min_index = target
        unsearched_nodes.remove(target_min_index) # 探索するので未探索リストから除去
        target_edge = route_list[target_min_index] # ターゲットになるノードからのびるエッジのリスト
        for index, route_dis in enumerate(target_edge):
            if route_dis != 0:
                if distance[index] > (distance[target_min_index] + route_dis):
                    distance[index] = distance[target_min_index] + route_dis # 過去に設定されたdistanceよりも小さい場合はdistanceを更新
                    if index != start:
                        previous_nodes[index] =  target_min_index #　ひとつ前に到達するノードのリストも更新

    # 以下で結果の表示
    print("-----経路-----")
    previous_node = terminal
    path = []
    while previous_node != -1:
        path.append(previous_node)
        previous_node = previous_nodes[previous_node]
    path.reverse()

    for node in path:
        if node != terminal:
            print(str(node) + " -> ", end='')
        else:
            print(str(node))     
    print("-----距離-----")
    print(distance[terminal])

有向辺、無向辺どちらでも使えると思います。

使用例

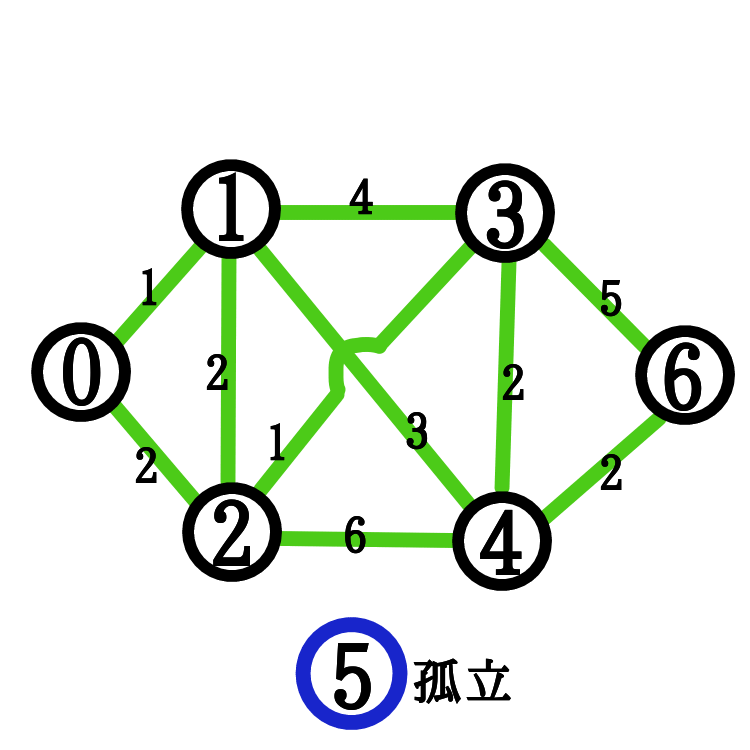
コード

route = [[0,1,2,0,0,0,0],
         [1,0,2,4,3,0,0],
         [2,2,0,1,6,0,0],
         [0,4,1,0,2,0,5],
         [0,3,6,2,0,0,2],
         [0,0,0,0,0,0,0],
         [0,0,0,5,2,0,0]]

dijkstra(route,0,6)
dijkstra(route,2,6)

出力結果

-----経路-----
0 -> 1 -> 4 -> 6
-----距離-----
6

-----経路-----
2 -> 3 -> 4 -> 6
-----距離-----
5

注意点と課題

細かい条件のエラーなどを考えていないので、
エラー等が出ましたら、教えていただけると嬉しいです。